Bonjour à tous,
Je rencontre un petit problème pour le chapitre des fonctions dérivées.
En fait j'ai plusieurs questions à vous soumettre :
1) Dans la formule de l'équation de la tangente, à savoir :
F'(a)(x-a)+F(a), que signifient chaque terme ?
Et surtout comment faire pour calculer l'équation d'une tangente ? 
(comment l'appliquer..)
2) Comment déterminer un nombre dérivé en fonction du coefficient directeur de la tangente ? Un exemple d'énoncé : "Déterminer graphiquement F'(0), F'(2) etc..."
Je ne sais pas comment le LIRE à partir du graphique.. (il me semble qu'il y une histoire de +1, -1...je ne sais plus
)
Merci d'avance, c'est assez urgent et je serais vraiment heureux d'obtenir des réponses.
tags :
posted the 02/26/2012 at 04:06 PM by
roby
home page | 
news | 
blogs | 
videos | 
reviews | 
previews | 
features | 
Facebook
profile
comments (19)
F'(a)=a
(x-a)=x
F(a)=b
il n'y a plus qu'a calculer et remplacer les a x et b
si la dérivé est positif, alors F(x) est croissante
si la dérivé est négative, f(x) est décroissante.
souvent quand on demande de déterminer graphiquement, c'est que la courbe f(x) change (croissante a décroissante ou le contraire) après, situ veux de l'aide, scan ta courbe!
F'(a) est l'image du nombre "a" par la fonction F', dérivée de la fonction F.
La tangente, en "a", a donc pour équation "F'(a)(x-a) + d" ou "F'(a)
- soit la droite tangente à la courbe en ce point est déjà tracé et on peut faire une lecture graphique ;
- soit la droite tangente à la courbe n'est pas tracée et il faut alors calculer la fonction dérivée de la fonction de départ et calculer, dans ton exemple, F'(-5).
pardon, je n'avais pas vu le graph.
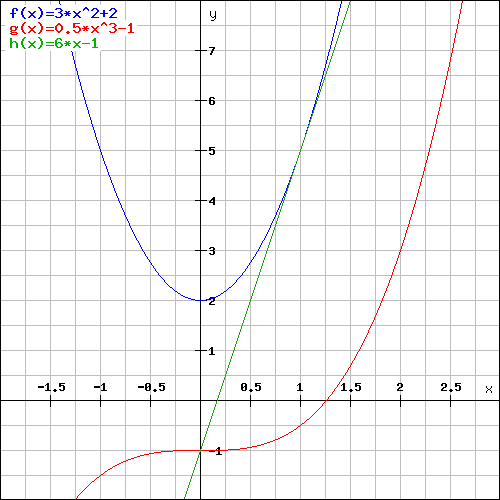
L'équation de la tangente est matquée en vert en haut à droite, le coefficient directeur vaut 6 donc f'(1) = 6.
y = f'(a)(x - a) + f(a).
y = f'(1)(x - 1) + f(1)
y = 6(x - 1) + f(1) f(1) = 3×1^2 + 2 = 3×1 + 2 = 3 + 2 = 5
y = 6(x -1) + 5.
On développe puis on réduit : y = 6x - 6 + 5
Finalement y = 6x - 1, c'est bien l'équation de droite donnée en vert.
Ce genre d'exercice était dans les plus simples au bac de maths il me semble.
14 en maths au bac alors que j'avais moins de la moyenne durant ma scolarité, sisi
Pour calculer par lecture graphique F'(2) par exemple tu place sur ta courbe un point
A'( 2 + 1 ; f(2)) ; et tu traces ensuite la droite disons D, parallèle à l'axe des ordonnées passant par A', ensuite appelons B l'intersection de la tangente F'(2) avec D, tu reportes la "distances" A'B sur l'axe des ordonnées et tu l'as ton F'(a)